有一个节日，它变化莫测，每年的日期都不一样，有可能是3月22日到4月25日之间的任何一天。这个节日，是纪念耶稣基督于公元30/33年被钉死后第三天复活，象征重生与希望。

它就是复活节——“每年春分月圆之后第一个星期日”。

复活节是世界上最难计算的节日。复活节计算和显示，也是最难解决的钟表问题之一。

（一）百达翡丽的专利

1985年12月13日，百达翡丽获得一项重要专利：按照基督教历法计算复活节日期。

大名鼎鼎的Calibre 89超级复杂怀表里，就装有这项专利机件。这是人类便携式时计历史上，第一次展示复活节日期。

Calibre 89诞生于1989年，庆祝百达翡丽150周年，这款怀表配备33项复杂功能，数量之多创造了便携式时计之最。

 这项专利的发明人，包括百达翡丽技术部门主管Jean-Pierre Musy, 在研发部工作的François Devaud和Frédérique Zesiger。控制复活节日期显示的核心，是一个有凹槽的轮，以凹槽深度的不同，对应不同的日期显示。Calibre 89可以准确显示从1989至2017的复活节日期。2017年之后，怀表必须回原厂保养，更换下一个29年的控制组件。  

那么问题来了，为什么百达翡丽不能一步到位，直接做成不用更换、循环显示复活节日历呢？

首先要回答一个问题，复活节多少年一循环？

（二）复活节多少年一循环

1582年10月，欧洲发生了一件怪事。

教宗格列高利十三世（Gregorius PP. XIII）颁布新的历法，同时宣布，10月4号的次日，不是5号，而是10月15号。一下子跳过10天，农民们非常不满，认为这是要剥削他们10天的房租。

这种全新的历法，就是格里历（Calendarium Gregorianum），我们一直沿用到今天，就是中文所讲的阳历、公历。

1582年采用新的历法，目的并不是剥削房租，而是因为旧的历法不够准确。旧的历法就是儒略历（Julian calendar）。儒略历资历甚老，诞生于罗马，早在公元前45年就开始起执行。儒略历的主要内容是：一年设12个月，大小月交替，四年一闰，平年365日，闰年于二月底增加一闰日，年平均长度为365.25日。

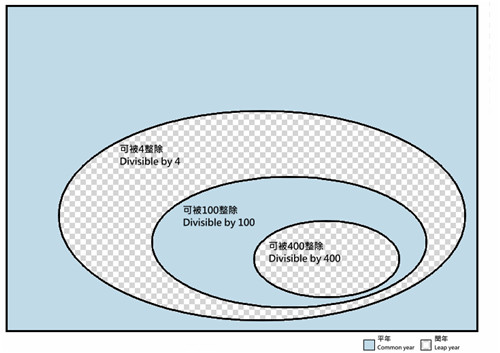
简单来说，两个历法的主要区别，是增加一条特别规定：除非能被400整除，所有的世纪年（能被100整除）都不设闰日。即：

1/ 公元年分非4的倍数，为平年。

2/ 公元年分为4的倍数但非100的倍数，为闰年。

3/ 公元年分为100的倍数但非400的倍数，为平年。

4/ 公元年分为400的倍数，为闰年。

那么，新的历法能把准确度提高多少呢？格里历的历年平均长度为365.2425日，接近平均回归年的365.242199074日，即每3300年误差一日，也更接近春分点回归年的365.24237日，即每8000年误差一日；而儒略历的历年为365.25日，每128年就误差一日。

此刻，是格里历的2020年4月11日，儒略历的2020年3月29日。

明白了格里历和儒略历的区别，我们来看复活节在两种历法下多少年一循环。

对古老的儒略历来说，复活节是532年一循环。

东西方历法有两个对应的概念：在西方， “默冬章”或“默冬周期”（Metonic cycle）是古希腊天文学家默冬发现的一个天文学周期，他生活在公元前5世纪的雅典。默冬发现，19个回归年（tropical year）的时间长度，和235个朔望月几乎相同。所以阴阳历若采十九年七闰法，每19年加入7个闰月，就可以协调回归年（太阳的周期）与朔望月（月亮的周期）间的时间差距，以较为简易的方式制历。中国古代也有同样的发现，并称此周期为一“章”。

1回归年 平均= 365.2421990741日 = 365天5小时48分46秒

1朔望月 平均= 29.530588日 = 29天12小时44分2.8秒

19个回归年 = 19 * 365.2421990741 = 6939.60178 日

235个朔望月 = 235 * 29.530588 = 6939.68818 日

儒略历中的复活节，需要19*4*7=532年才能循环一次。4代表闰年，7代表每周7天。

而对于更准确的格里历来说，这个循环需要惊人的5,700,000年！

大家已经明白，百达翡丽无法做出一个有532个凹痕的儒略历程序轮，让它循环运转，何况儒略历在这个地球的绝大多数地方已经不再使用。更不可能做一个有5,700,000个凹痕的，那样的话，怀表要比足球场还大。

下图是格里历完整的5,700,000年周期复活节日期的分布。4月19日以3.87%的概率拔得头筹。3月22日是最不容易遇到的复活节，仅有0.48%概率。2020年的复活节是4月12日。

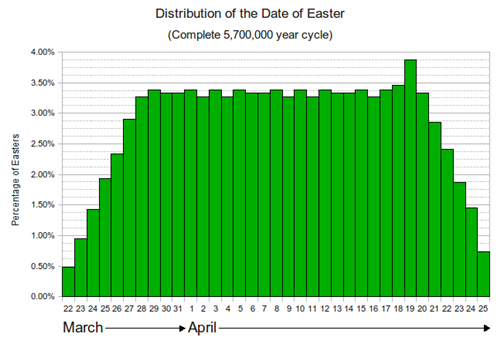
顺便说一下，1582年教宗推广新历法的时候，只有意大利、波兰、西班牙、葡萄牙马上使用。因为新历法是教宗颁布的，新教国家予以抵制。直到1752年，大英帝国以及现在美国的一部分才开始采用格里历，中国则要晚到1912年。

（三）复活节怎么计算

相信这个问题已经在大家头脑中盘绕许久了。简而言之，非常复杂。 

这里翻译一种运算方法。选择公历的任何年份，将其命名为X。要确定当年的复活节日期，请执行以下10个计算：

1/ 将X除以19，得到一个商（我们忽略）和余数A。这是该年在19年农历周期中的位置。A +1是当年的黄金数字。

2/ 用X除以100，得到商B和余数C。

3/ 用B除以4，得到商D和余数E。

4/ 用8B + 13除以25，得到商G和余数（我们忽略）。

5/ 计算19A + B – D – G + 15，将结果除以30，得到一个商（我们忽略）和余数H。当H小于24时，该年实际值为23 – H，否则，则为53 –H。

6/ 计算A + 11H，再除以319，得到商M和余数（我们忽略）。

7/ 用C除以4，得到商J和余数K。

8/ 计算2E + 2J – K – H + M + 32，除以7，得到商（我们忽略）和余数L。

9/ 计算H – M + L + 90，除以25，得出商N和余数（我们忽略）。

10/ 计算H – M + L + N + 19，除以32，得到一个商（我们忽略）和余数P。

复活节周日，就是第N个月的第P天。可以用2E + 2J-K除以7并乘以余数（0等于字母A，1等于B，依此类推）来找到年份的主字母。

让我们为X= 2001尝试这种方法：（1）A = 6; （2）B = 20，C = 1；（3）D = 5，E = 0；（4）G = 6；（5）H = 18；（6）M = 0；（7）J = 0，K = 1；（8）L = 6；（9）N = 4；（10）P =15。因此2001年复活节是4月15日。

我们检查一下格里历复活节4月15日的对应年份，确实有2001。

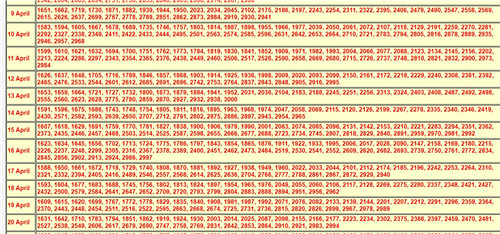
自古以来，复活节的算法都非常复杂。拉丁文里面表示“计算”的词，Computus，就是专指计算复活节的方法。

下图来自瑞典，用来计算1140至1671年的复活节日期。有人说：“许多迹象表明，在中世纪的欧洲，数学的唯一重要应用，就是计算复活节日期。”

除了怀表，复活节日期也在天文钟上得到体现，不得不感慨古人的智慧！比如法国东部美丽的小城斯特拉斯堡（Strasbourg）的主教座堂里，就有一座这样的天文钟。复活节日期的计算机制，位于最底部之左边。关于这座钟表史上的伟大杰作，可阅读拙文《欧洲游记：斯特拉斯堡天文钟》。

（四）复活节怎么过

在德国，复活节是这么过的：彩蛋必不可少，大人要在复活节星期日那天，把彩蛋藏在花园里，让孩子们去寻找。是谁带来了复活节彩蛋呢？人们说是兔子。兔子也被视为春的使者。有些地方会举办游行（当然今年不行），重演当年耶稣受刑殉难的过程。复活节还有篝火，这一习俗来源于日耳曼游牧民族，熊熊燃烧的火焰不仅要赶走寒冬，也要驱赶恶灵。希望还能赶走COVID-19！

最后，在复活节周日（Ostersonntag），教堂钟声敲响，宣告耶稣复活的消息。(图：1887年的德国乌尔姆大教堂外景，19世纪教堂内景。)

复活节，象征着重生与希望。又一个复活节在欧洲度过，这里万物复苏，阳光明媚。当钟声响起，又将带来满满希望，期待这一刻降临！

老菲烈 & Christina

2020年4月11日，慕尼黑

羽毫钟表收藏 Yuhao Time

举千钧若扛一羽，拥万物若携微毫。

原创文章，未经许可，不可转载。